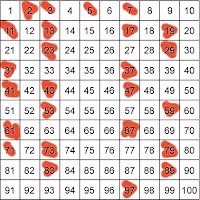
La cuestión acerca de si el número 1 debe ser considerado un número primo no ha estado exenta de polémica:
Hasta el siglo XIX la mayor parte de los matemáticos consideraban primo al número uno. Por ejemplo, la lista de números primos de Derrick Norman Lehmer publicada hasta el año 1956 comenzando con el número 1 (esta lista incluía todos los primos hasta el 10.006.721). Sin embargo, se dice que Henri Lebesgue (1875 - 1941) fue el último matemático en llamar primo al número 1.
Por qué el uno no es primo
Y es que, a pesar de que muchos teoremas matemáticos que hacen referencia a los números primos se siguen cumpliendo si incluimos el 1 en la lista, hay otros que no. Por ejemplo, si el número uno fuera admitido como número primo, el número 15 se podría factorizar como 3·5 o como 1·3·5. Por lo tanto tendría dos factorizaciones diferentes en números primos, invalidando así el Teorema fundamental de la aritmética:"Todo número natural tiene una representación única como producto de factores primos, salvo por su orden."Además de esto, los números primos presentan varias propiedades de las que carece el número 1, tales como la relación del número con el valor correspondiente de la función divisor o con la función φ de Euler.
Saber más: 1






